A Discussion of 'Adversarial Examples Are Not Bugs, They Are Features': Discussion and Author Responses

This article is part of a discussion of the Ilyas et al. paper “Adversarial examples are not bugs, they are features”. You can learn more in the main discussion article .

Other Comments Comment by Ilyas et al.

We want to thank all the commenters for the discussion and for spending time designing experiments analyzing, replicating, and expanding upon our results. These comments helped us further refine our understanding of adversarial examples (e.g., by visualizing useful non-robust features or illustrating how robust models are successful at downstream tasks), but also highlighted aspects of our exposition that could be made more clear and explicit.

Our response is organized as follows: we first recap the key takeaways from our paper, followed by some clarifications that this discussion brought to light. We then address each comment individually, prefacing each longer response with a quick summary.

We also recall some terminology from our paper that features in our responses:

Datasets: Our experiments involve the following variants of the given dataset $D$ (consists of sample-label pairs ( $x$ , $y$ )) The exact details for construction of the datasets can be found in our paper, and the datasets themselves can be downloaded at http://git.io/adv-datasets :

$\widehat{\mathcal{D}}_{R}$ : Restrict each sample $x$ to features that are used by a robust model.
$\widehat{\mathcal{D}}_{NR}$ : Restrict each sample $x$ to features that are used by a standard model.
$\widehat{\mathcal{D}}_{det}$ : Adversarially perturb each sample $x$ using a standard model in a consistent manner towards class $y + 1\mod C$ .
$\widehat{\mathcal{D}}_{rand}$ : Adversarially perturb each sample $x$ using a standard model towards a uniformly random class.

Main points

Takeaway #1: Adversarial examples as innate brittleness vs. useful features (sensitivity vs reliance)

The goal of our experiments with non-robust features is to understand how adversarial examples fit into the following two worlds:

World 1: Adversarial examples exploit directions irrelevant for classification. In this world, adversarial examples arise from sensitivity to a signal that is unimportant for classification. For instance, suppose there is a feature $f(x)$ that is not generalizing on the dataNote that $f(x)$ could be correlated with the label in the training set but not in expectation/on the test set., but the model for some reason puts a lot of weight on it, i.e., this sensitivity is an aberration “hallucinated” by the model. Adversarial examples correspond to perturbing the input to change this feature by a small amount. This perturbation, however, would be orthogonal to how the model actually typically makes predictions (on natural data). (Note that this is just a single illustrative example — the key characteristic of this world is that features “flipped” when making adversarial examples are separate from the ones actually used to classify inputs.)
World 2: Adversarial examples exploit features that are useful for classification. In this world, adversarial perturbations can correspond to changes in the input that manipulate features relevant to classification. Thus, models base their (mostly correct) predictions on features that can be altered via small perturbations.

Recent works provide some theoretical evidence that adversarial examples can arise from finite-sample overfitting or other concentration of measure-based phenomena, thus supporting the “World 1” viewpoint on adversarial examples. The question is: is “World 1” the right way to think about adversarial examples? If so, this would be good news — under this mindset, adversarial robustness might just be a matter of getting better, “bug-free” models (for example, by reducing overfitting).

Our findings show, however, that the “World 1” mindset alone does not fully capture adversarial vulnerability; “World 2“ must be taken into account. Adversarial examples can — and do, if generated via standard methods — rely on “flipping” features that are actually useful for classification. Specifically, we show that by relying only on perturbations corresponding to standard first-order adversarial attacks one can learn models that generalize to the test set. This means that these perturbations truly correspond to directions that are relevant for classifying new, unmodified inputs from the dataset. In summary, our message is:

Adversarial vulnerability can arise from flipping features in the data that are useful for classification of correct inputs.

In particular, note that our experiments (training on the $\widehat{\mathcal{D}}_{rand}$ and $\widehat{\mathcal{D}}_{det}$ datasets) would not have the same result in World 1. Concretely, in the “cartoon example” of World 1 presented above, the classifier puts large weight $w$ on a feature coordinate $f(x)$ that is not generalizing for “natural images.” Then, adversarial examples towards either class can be made by simply making $f(x)$ slightly positive or slightly negative. However, a classifier learned from these adversarial examples would not generalize to the true dataset (since it would learn to depend on a feature that is not useful on natural images).

Takeaway #2: Learning from “meaningless” data

Another implication of our experiments is that models may not even need any information which we as humans view as “meaningful” in order to do well (in the generalization sense) on standard image datasets. (Our $\widehat{\mathcal{D}}_{NR}$ dataset is a perfect example of this.)

Takeaway #3: Cannot fully attribute adversarial examples to X

We also show that we cannot conclusively fully attribute adversarial examples to any specific aspect of the standard training framework (BatchNorm, ResNets, SGD, etc.). In particular, our “robust dataset” $\widehat{\mathcal{D}}_{R}$ is a counterexample to any claim of the form “given any dataset, training with BatchNorm/SGD/ResNets/overparameterization/etc. leads to adversarial vulnerability” (as classifiers with all of these components, when trained on $\widehat{\mathcal{D}}_{R}$ , generalize robustly to CIFAR-10). In that sense, the dataset clearly plays a role in the emergence of adversarial examples. (Also, further corroborating this is Preetum’s “adversarial squares” dataset here, where standard networks do not become adversarially vulnerable as long as there is no label noise or overfitting.)

A Few Clarifications

In addition to further refining our understanding of adversarial examples, the comments were also very useful in pointing out which aspects of our claims could benefit from further clarification. To this end, we make these clarifications below in the form of a couple “non-claims” — claims that we did not intend to make. We’ll also update our paper in order to make these clarifications explicit.

Non-Claim #1: “Adversarial examples cannot be bugs”

Our goal is to say that since adversarial examples can arise from well-generalizing features, simply patching up the “bugs” in ML models will not get rid of adversarial vulnerability — we also need to make sure our models learn the right features. This, however, does not mean that adversarial vulnerability cannot arise from “bugs”. In fact, note that several papers have proven that adversarial vulnerability can arise from what we refer to as “bugs,” e.g. finite-sample overfitting, concentration of measure, high dimensionality, etc. Furthermore, We would like to thank Preetum for pointing out that this issue may be a natural misunderstanding, and for exploring this point in even more depth in his response below.

Non-Claim #2: “Adversarial examples are purely a result of the dataset”

Even though we demonstrated that datasets do play a role in the emergence of adversarial examples, we do not intend to claim that this role is exclusive. In particular, just because the data admits non-robust functions that are well-generalizing (useful non-robust features), doesn’t mean that any model will learn to pick up these features. For example, it could be that the well-generalizing features that cause adversarial examples are only learnable by certain architectures. However, we do show that there is a way, via only altering the dataset, to induce robust models — thus, our results indicate that adversarial vulnerability indeed cannot be completely disentangled from the dataset (more on this in Takeaway #3).

The following responses may also be viewed in context with the comment they’re addressing. Return to the discussion article for a list of summaries.

Responses to comments

Adversarial Example Researchers Need to Expand What is Meant by “Robustness” (Dan Hendrycks, Justin Gilmer)

Response Summary: The demonstration of models that learn from only high-frequency components of the data is an interesting finding that provides us with another way our models can learn from data that appears “meaningless” to humans. The authors fully agree that studying a wider notion of robustness will become increasingly important in ML, and will help us get a better grasp of features we actually want our models to rely on.

Response: The fact that models can learn to classify correctly based purely on the high-frequency component of the training set is neat! This nicely complements one of our takeaways: models will rely on useful features even if these features appear incomprehensible to humans.

Also, while non-robustness to noise can be an indicator of models using non-robust useful features, this is not how the phenomenon was predominantly viewed. More often than not, the brittleness of ML models to noise was instead regarded as an innate shortcoming of the models, e.g., due to poor margins. (This view is even more prevalent in the adversarial robustness community.) Thus, it was often expected that progress towards “better”/”bug-free” models will lead to them being more robust to noise and adversarial examples.

Finally, we fully agree that the set of $L_p$ -bounded perturbations is a very small subset of the perturbations we want our models to be robust to. Note, however, that the focus of our work is human-alignment — to that end, we demonstrate that models rely on features sensitive to patterns that are imperceptible to humans. Thus, the existence of other families of incomprehensible but useful features would provide even more support for our thesis — identifying and characterizing such features is an interesting area for future research.

Robust Feature Leakage (Gabriel Goh)

Response Summary: This is a nice in-depth investigation that highlights (and neatly visualizes) one of the motivations for designing the $\widehat{\mathcal{D}}_{det}$ dataset.

Response: This comment raises a valid concern which was in fact one of the primary reasons for designing the $\widehat{\mathcal{D}}_{det}$ dataset. In particular, recall the construction of the $\widehat{\mathcal{D}}_{rand}$ dataset: assign each input a random target label and do PGD towards that label. Note that unlike the $\widehat{\mathcal{D}}_{det}$ dataset (in which the target class is deterministically chosen), the $\widehat{\mathcal{D}}_{rand}$ dataset allows for robust features to actually have a (small) positive correlation with the label.

To see how this can happen, consider the following simple setting: we have a single feature $f(x)$ that is $1$ for cats and $-1$ for dogs. If $\epsilon = 0.1$ then $f(x)$ is certainly a robust feature. However, randomly assigning labels (as in the dataset $\widehat{\mathcal{D}}_{rand}$ ) would make this feature uncorrelated with the assigned label, i.e., we would have that $E[f(x)\cdot y] = 0$ . Performing a targeted attack might in this case induce some correlation with the assigned label, as we could have $\mathbb{E}[f(x+\eta\cdot\nabla f(x))\cdot y] > \mathbb{E}[f(x)\cdot y] = 0$ , allowing a model to learn to correctly classify new inputs.

In other words, starting from a dataset with no features, one can encode robust features within small perturbations. In contrast, in the $\widehat{\mathcal{D}}_{det}$ dataset, the robust features are correlated with the original label (since the labels are permuted) and since they are robust, they cannot be flipped to correlate with the newly assigned (wrong) label. Still, the $\widehat{\mathcal{D}}_{rand}$ dataset enables us to show that (a) PGD-based adversarial examples actually alter features in the data and (b) models can learn from human-meaningless/mislabeled training data. The $\widehat{\mathcal{D}}_{det}$ dataset, on the other hand, illustrates that the non-robust features are actually sufficient for generalization and can be preferred over robust ones in natural settings.

The experiment put forth in the comment is a clever way of showing that such leakage is indeed possible. However, we want to stress (as the comment itself does) that robust feature leakage does not have an impact on our main thesis — the $\widehat{\mathcal{D}}_{det}$ dataset explicitly controls for robust feature leakage (and in fact, allows us to quantify the models’ preference for robust features vs non-robust features — see Appendix D.6 in the paper).

Two Examples of Useful, Non-Robust Features (Gabriel Goh)

Response Summary: These experiments with linear models are a great first step towards visualizing non-robust features for real datasets (and thus a neat corroboration of their existence). Furthermore, the theoretical construction of “contaminated” non-robust features opens an interesting direction of developing a more fine-grained definition of features.

Response: These experiments (visualizing the robustness and usefulness of different linear features) are very interesting! They both further corroborate the existence of useful, non-robust features and make progress towards visualizing what these non-robust features actually look like.

We also appreciate the point made by the provided construction of non-robust features (as defined in our theoretical framework) that are combinations of useful+robust and useless+non-robust features. Our theoretical framework indeed enables such a scenario, even if — as the commenter already notes — our experimental results do not. (In this sense, the experimental results and our main takeaway are actually stronger than our theoretical framework technically captures.) Specifically, in such a scenario, during the construction of the $\widehat{\mathcal{D}}_{det}$ dataset, only the non-robust and useless term of the feature would be flipped. Thus, a classifier trained on such a dataset would associate the predictive robust feature with the wrong label and would thus not generalize on the test set. In contrast, our experiments show that classifiers trained on $\widehat{\mathcal{D}}_{det}$ do generalize.

Overall, our focus while developing our theoretical framework was on enabling us to formally describe and predict the outcomes of our experiments. As the comment points out, putting forth a theoretical framework that captures non-robust features in a very precise way is an important future research direction in itself.

Adversarially Robust Neural Style Transfer (Reiichiro Nakano)

Response Summary: Very interesting results that highlight the potential role of non-robust features and the utility of robust models for downstream tasks. We’re excited to see what kind of impact robustly trained models will have in neural network art! Inspired by these findings, we also take a deeper dive into (non-robust) VGG, and find some interesting links between robustness and style transfer.

Response: These experiments are really cool! It is interesting that preventing the reliance of a model on non-robust features improves performance on style transfer, even without an explicit task-related objective (i.e. we didn’t train the networks to be better for style transfer).

We also found the discussion of VGG as a “mysterious network” really interesting — it would be valuable to understand what factors drive style transfer performance more generally. Though not a complete answer, we made a couple of observations while investigating further:

Style transfer does work with AlexNet: One wrinkle in the idea that robustness is the “secret ingredient” to style transfer could be that VGG is not the most naturally robust network — AlexNet is. However, based on our own testing, style transfer does seem to work with AlexNet out-of-the-box, as long as we use a few early layers in the network (in a similar manner to VGG):

Style transfer using AlexNet, using conv_1 through conv_4.

Observe that even though style transfer still works, there are checkerboard patterns emerging — this seems to be a similar phenomenon to the one noticed in the comment in the context of robust models. This might be another indication that these two phenomena (checkerboard patterns and style transfer working) are not as intertwined as previously thought.

From prediction robustness to layer robustness: Another potential wrinkle here is that both AlexNet and VGG are not that much more robust than ResNets (for which style transfer completely fails), and yet seem to have dramatically better performance. To try to explain this, recall that style transfer is implemented as a minimization of a combined objective consisting of a style loss and a content loss. We found, however, that the network we use to compute the style loss is far more important than the one for the content loss. The following demo illustrates this — we can actually use a non-robust ResNet for the content loss and everything works just fine:

Style transfer seems to be rather invariant to the choice of content network used, and very sensitive to the style network used.

Therefore, from now on, we use a fixed ResNet-50 for the content loss as a control, and only worry about the style loss.

Now, note that the way that style loss works is by using the first few layers of the relevant network. Thus, perhaps it is not about the robustness of VGG’s predictions, but instead about the robustness of the layers that we actually use for style transfer?

To test this hypothesis, we measure the robustness of a layer $f$ as:

R(f) = \frac{\mathbb{E}_{x_1\sim D}\left[\max_{x’} \|f(x’) - f(x_1)\|_2 \right]} {\mathbb{E}_{x_1, x_2 \sim D}\left[\|f(x_1) - f(x_2)\|_2\right]}

Essentially, this quantity tells us how much we can change the output of that layer $f(x)$ within a small ball, normalized by how far apart representations are between images in general. We’ve plotted this value for the first few layers in a couple of different networks below:

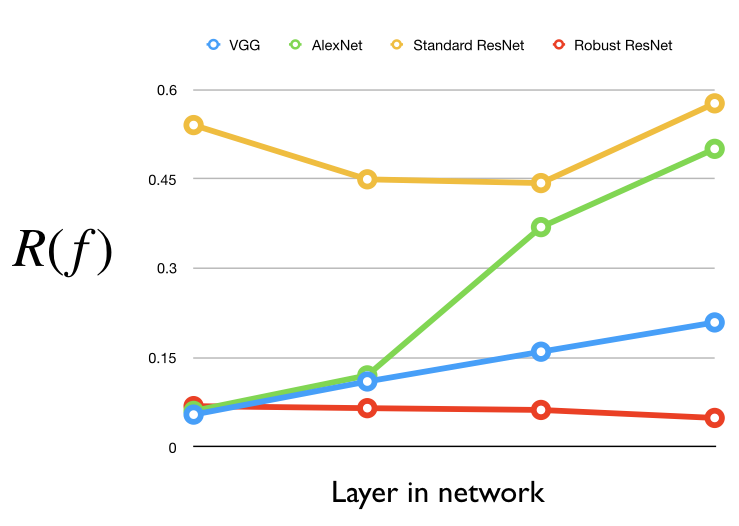
The robustness $R(f)$ of the first four layers of VGG16, AlexNet, and robust/standard ResNet-50 trained on ImageNet.

Here, it becomes clear that, the first few layers of VGG and AlexNet are actually almost as robust as the first few layers of the robust ResNet! This is perhaps a more convincing indication that robustness might have something to with VGG’s success in style transfer after all.

Finally, suppose we restrict style transfer to only use a single layer of the network when computing the style lossUsually style transfer uses several layers in the loss function to get the most visually appealing results — here we’re only interested in whether or not style transfer works (i.e. actually confers some style onto the image).. Again, the more robust layers seem to indeed work better for style transfer! Since all of the layers in the robust ResNet are robust, style transfer yields non-trivial results even using the last layer alone. Conversely, VGG and AlexNet seem to excel in the earlier layers (where they are non-trivially robust) but fail when using exclusively later (non-robust) layers:

Style transfer using a single layer. The names of the layers and their robustness $R(f)$ are printed below each style transfer result. We find that for both networks, the robust layers seem to work (for the robust ResNet, every layer is robust).

Of course, there is much more work to be done here, but we are excited to see further work into understanding the role of both robustness and the VGG in network-based image manipulation.

Adversarial Examples are Just Bugs, Too (Preetum Nakkiran)

Response Summary: A fine-grained look at adversarial examples that neatly complements our thesis (i.e. that non-robust features exist and adversarial examples arise from them, see Takeaway #1) while providing an example of adversarial examples that arise from “bugs”. The fact that the constructed “bugs”-based adversarial examples don’t transfer constitutes another evidence for the link between transferability and (non-robust) features.

Response: As mentioned above, we did not intend to claim that adversarial examples arise exclusively from (useful) features but rather that useful non-robust features exist and are thus (at least partially) responsible for adversarial vulnerability. In fact, prior work already shows how in theory adversarial examples can arise from insufficient samples or finite-sample overfitting , and the experiments presented here (particularly, the adversarial squares) constitute a neat real-world demonstration of these facts.

Our main thesis that “adversarial examples will not just go away as we fix bugs in our models” is not contradicted by the existence of adversarial examples stemming from “bugs.” As long as adversarial examples can stem from non-robust features (which the commenter seems to agree with), fixing these bugs will not solve the problem of adversarial examples.

Moreover, with regards to feature “leakage” from PGD, recall that in or D_det dataset, the non-robust features are associated with the correct label whereas the robust features are associated with the wrong one. We wanted to emphasize that, as shown in [Appendix D.6](LINK), models trained on our D_det dataset actually generalize better to the non-robust feature-label association that to the robust feature-label association. In contrast, if PGD introduced a small “leakage” of non-robust features, then we would expect the trained model would still predominantly use the robust feature-label association.

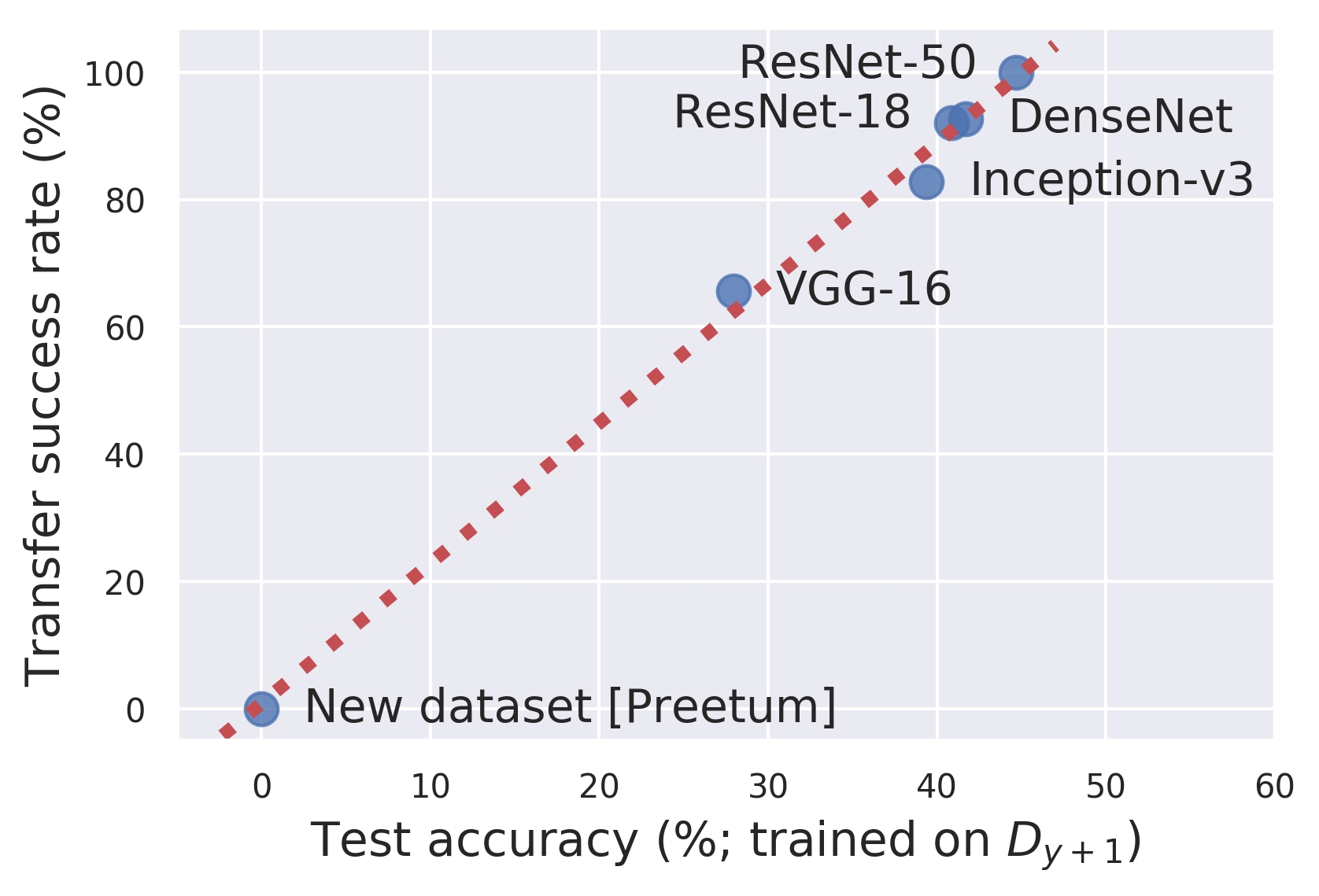
That said, the experiments cleverly zoom in on some more fine-grained nuances in our understanding of adversarial examples. One particular thing that stood out to us is that by creating a set of adversarial examples that are explicitly non-transferable, one also prevents new classifiers from learning features from that dataset. This finding thus makes the connection between transferability of adversarial examples and their containing generalizing features even stronger! Indeed, we can add the constructed dataset into our “ $\widehat{\mathcal{D}}_{det}$ learnability vs transferability” plot (Figure 3 in the paper) — the point corresponding to this dataset fits neatly onto the trendline!

Relationship between models reliance on non-robust features and their susceptibility to transfer attacks

Learning from Incorrectly Labeled Data (Eric Wallace)

Response Summary: These experiments are a creative demonstration of the fact that the underlying phenomenon of learning features from “human-meaningless” data can actually arise in a broad range of settings.

Response: Since our experiments work across different architectures, “distillation” in weight space cannot arise. Thus, from what we understand, the “distillation” hypothesis suggested here is referring to “feature distillation” (i.e. getting models which use the same features as the original), which is actually precisely our hypothesis too. Notably, this feature distillation would not be possible if adversarial examples did not rely on “flipping” features that are good for classification (see World 1 and World 2) — in that case, the distilled model would only use features that generalize poorly, and would thus generalize poorly itself.

Moreover, we would argue that in the experiments presented (learning from mislabeled data), the same kind of distillation is happening. For instance, a moderately accurate model might associate “green background” with “frog” thus labeling “green” images as “frogs” (e.g., the horse in the comment’s figure). Training a new model on this dataset will thus associate “green” with “frog” achieving non-trivial accuracy on the test set (similarly for the “learning MNIST from Fashion-MNIST” experiment in the comment). This corresponds exactly to learning features from labels, akin to how deep networks “distill” a good decision boundary from human annotators. In fact, we find these experiments a very interesting illustration of feature distillation that complements our findings.

We also note that an analogy to logistic regression here is only possible due to the low VC-dimension of linear classifiers (namely, these classifiers have dimension $d$ ). In particular, given any classifier with VC-dimension $k$ , we need at least $k$ points to fully specify the classifier. Conversely, neural networks have been shown to have extremely large VC-dimension (in particular, bigger than the size of the training set ). So even though labelling $d+1$ random points model-consistently is sufficient to recover a linear model, it is not necessarily sufficient to recover a deep neural network. For instance, Milli et al. are not able to reconstruct a ResNet-18 using only its predictions on random Gaussian inputs. (Note that we are using a ResNet-50 in our experiments.)

Finally, it seems that the only potentially problematic explanation for our experiments (namely, that enough model-consistent points can recover a classifier) is disproved by the experiment done by Preetum (see LINK). In particular, Preetum is able to design a dataset where training on mislabeled inputs that are model-consistent does not at all recover the decision boundary of the original model. More generally, the “model distillation” perspective raised here is unable to distinguish between the dataset created by Preetum below, and those created with standard PGD (as in our $\widehat{\mathcal{D}}_{det}$ and $\widehat{\mathcal{D}}_{rand}$ datasets).

Acknowledgments

We are deeply grateful to all of the commenters for their valuable responses and the ensuing discussions.

References

A boundary tilting persepective on the phenomenon of adversarial examples
Tanay, T. and Griffin, L., 2016. arXiv preprint arXiv:1608.07690.
Adversarially Robust Generalization Requires More Data
Schmidt, L., Santurkar, S., Tsipras, D., Talwar, K. and M{\k{a}}dry, A., 2018. Advances in Neural Information Processing Systems (NeurIPS).
Adversarial spheres
Gilmer, J., Metz, L., Faghri, F., Schoenholz, S.S., Raghu, M., Wattenberg, M. and Goodfellow, I., 2018. Workshop of International Conference on Learning Representations (ICLR).
Adversarial vulnerability for any classifier
Fawzi, A., Fawzi, H. and Fawzi, O., 2018. NeurIPS.
The curse of concentration in robust learning: Evasion and poisoning attacks from concentration of measure
Mahloujifar, S., Diochnos, D.I. and Mahmoody, M., 2019. AAAI.
Are adversarial examples inevitable?
Shafahi, A., Huang, W.R., Studer, C., Feizi, S. and Goldstein, T., 2019. ICLR.
Understanding deep learning requires rethinking generalization
Zhang, C., Bengio, S., Hardt, M., Recht, B. and Vinyals, O., 2016. International Conference on Learning Representations (ICLR).
Model reconstruction from model explanations
Milli, S., Schmidt, L., Dragan, A.D. and Hardt, M., 2018. arXiv preprint arXiv:1807.05185.

Updates and Corrections

If you see mistakes or want to suggest changes, please create an issue on GitHub.

Reuse

Diagrams and text are licensed under Creative Commons Attribution CC-BY 4.0 with the source available on GitHub, unless noted otherwise. The figures that have been reused from other sources don’t fall under this license and can be recognized by a note in their caption: “Figure from …”.

Citation

For attribution in academic contexts, please cite this work as

Engstrom, et al., "A Discussion of 'Adversarial Examples Are Not Bugs, They Are Features': Discussion and Author Responses", Distill, 2019.

BibTeX citation

@article{engstrom2019a,
  author = {Engstrom, Logan and Ilyas, Andrew and Madry, Aleksander and Santurkar, Shibani and Tran, Brandon and Tsipras, Dimitris},
  title = {A Discussion of 'Adversarial Examples Are Not Bugs, They Are Features': Discussion and Author Responses},
  journal = {Distill},
  year = {2019},
  note = {https://distill.pub/2019/advex-bugs-discussion/original-authors},
  doi = {10.23915/distill.00019.7}
}

[tanay2016boundary] A boundary tilting persepective on the phenomenon of adversarial examples
Tanay, T. and Griffin, L., 2016. arXiv preprint arXiv:1608.07690.

[schmidt2018adversarially] Adversarially Robust Generalization Requires More Data
Schmidt, L., Santurkar, S., Tsipras, D., Talwar, K. and M{\k{a}}dry, A., 2018. Advances in Neural Information Processing Systems (NeurIPS).

[gilmer2018adversarial] Adversarial spheres
Gilmer, J., Metz, L., Faghri, F., Schoenholz, S.S., Raghu, M., Wattenberg, M. and Goodfellow, I., 2018. Workshop of International Conference on Learning Representations (ICLR).

[fawzi2018adversarial] Adversarial vulnerability for any classifier
Fawzi, A., Fawzi, H. and Fawzi, O., 2018. NeurIPS.

[mahloujifar2018curse] The curse of concentration in robust learning: Evasion and poisoning attacks from concentration of measure
Mahloujifar, S., Diochnos, D.I. and Mahmoody, M., 2019. AAAI.

[shafahi2018are] Are adversarial examples inevitable?
Shafahi, A., Huang, W.R., Studer, C., Feizi, S. and Goldstein, T., 2019. ICLR.

[zhang2016understanding] Understanding deep learning requires rethinking generalization
Zhang, C., Bengio, S., Hardt, M., Recht, B. and Vinyals, O., 2016. International Conference on Learning Representations (ICLR).

[milli2018model] Model reconstruction from model explanations
Milli, S., Schmidt, L., Dragan, A.D. and Hardt, M., 2018. arXiv preprint arXiv:1807.05185.