The Grand Tour
Introduction
Deep neural networks often achieve best-in-class performance in supervised learning contests such as the ImageNet Large Scale Visual Recognition Challenge (ILSVRC)
To understand a neural network, we often try to observe its action on input examples (both real and synthesized)
Working Examples
To illustrate the technique we will present, we trained deep neural
network models (DNNs) with 3 common image classification datasets:
MNIST
 Image credit to https://en.wikipedia.org/wiki/File:MnistExamples.png
Image credit to https://en.wikipedia.org/wiki/File:MnistExamples.png
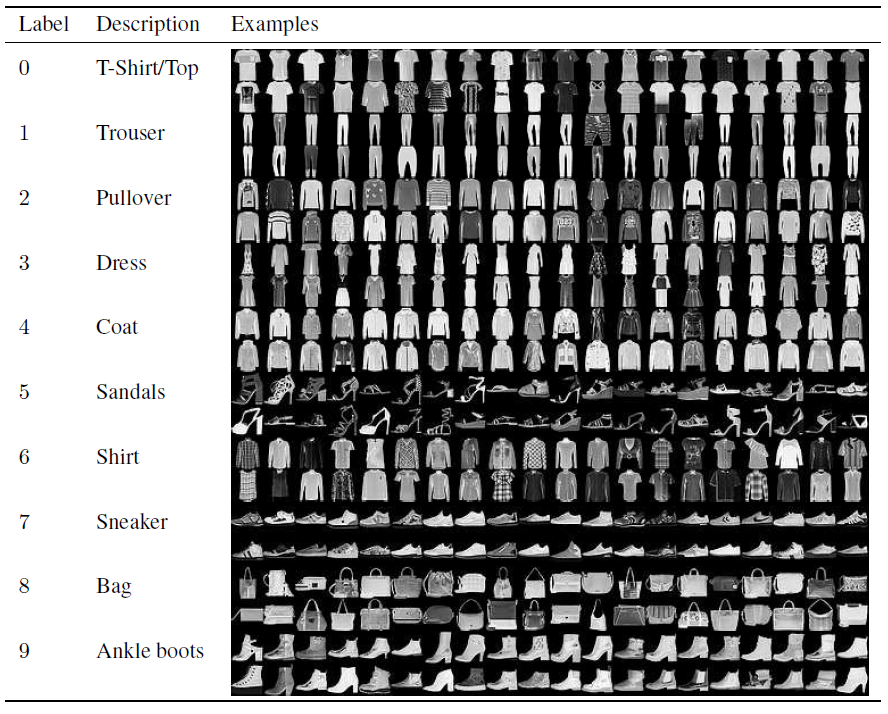 Image credit to https://towardsdatascience.com/multi-label-classification-and-class-activation-map-on-fashion-mnist-1454f09f5925
Image credit to https://towardsdatascience.com/multi-label-classification-and-class-activation-map-on-fashion-mnist-1454f09f5925
 Image credit to https://www.cs.toronto.edu/~kriz/cifar.html
Image credit to https://www.cs.toronto.edu/~kriz/cifar.html
The following figure presents a simple functional diagram of the neural network we will use throughout the article. The neural network is a sequence of linear (both convolutional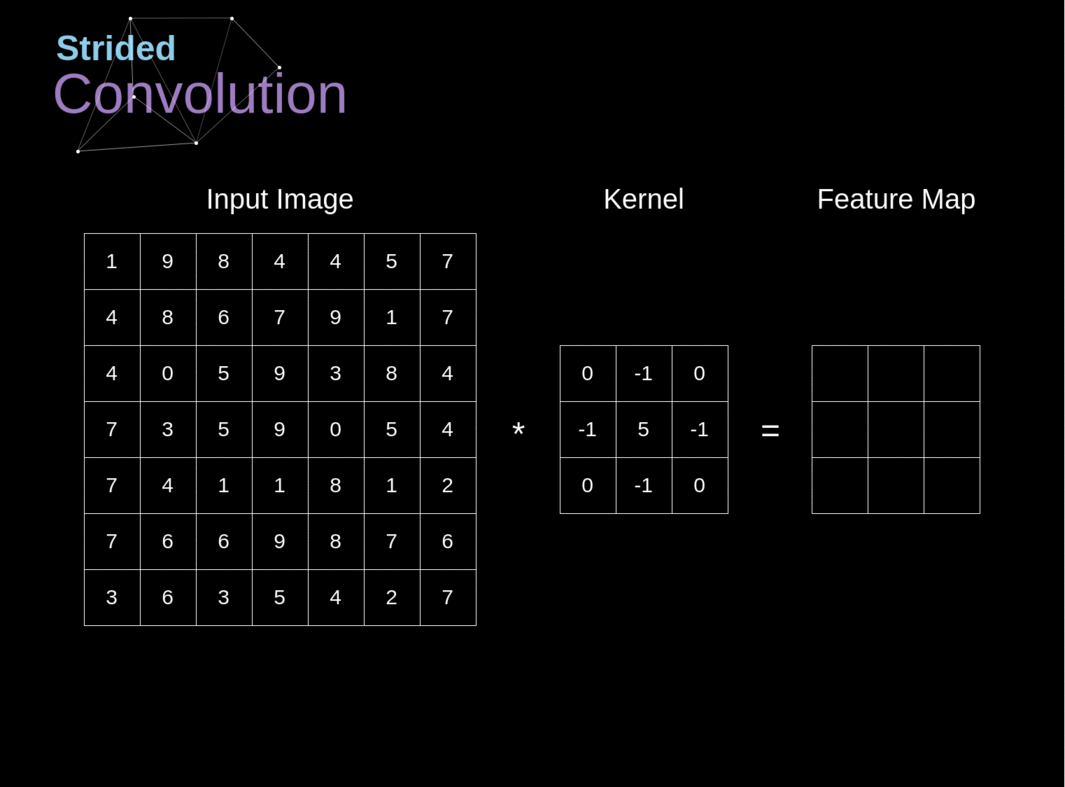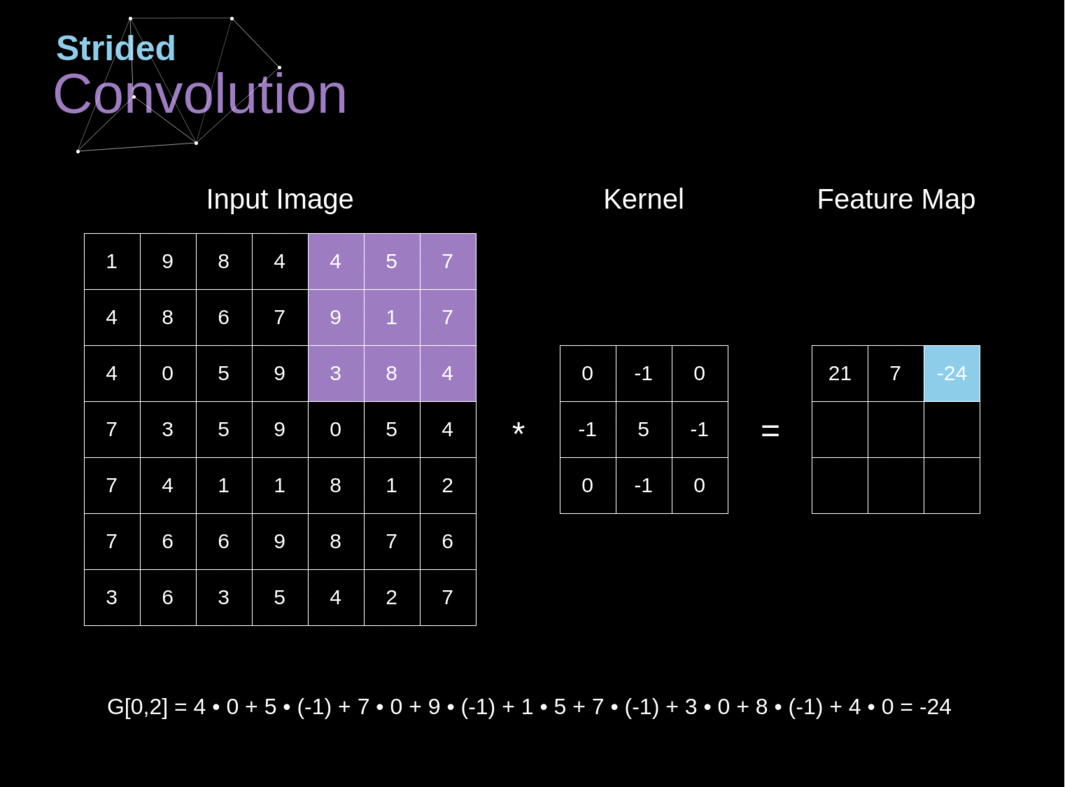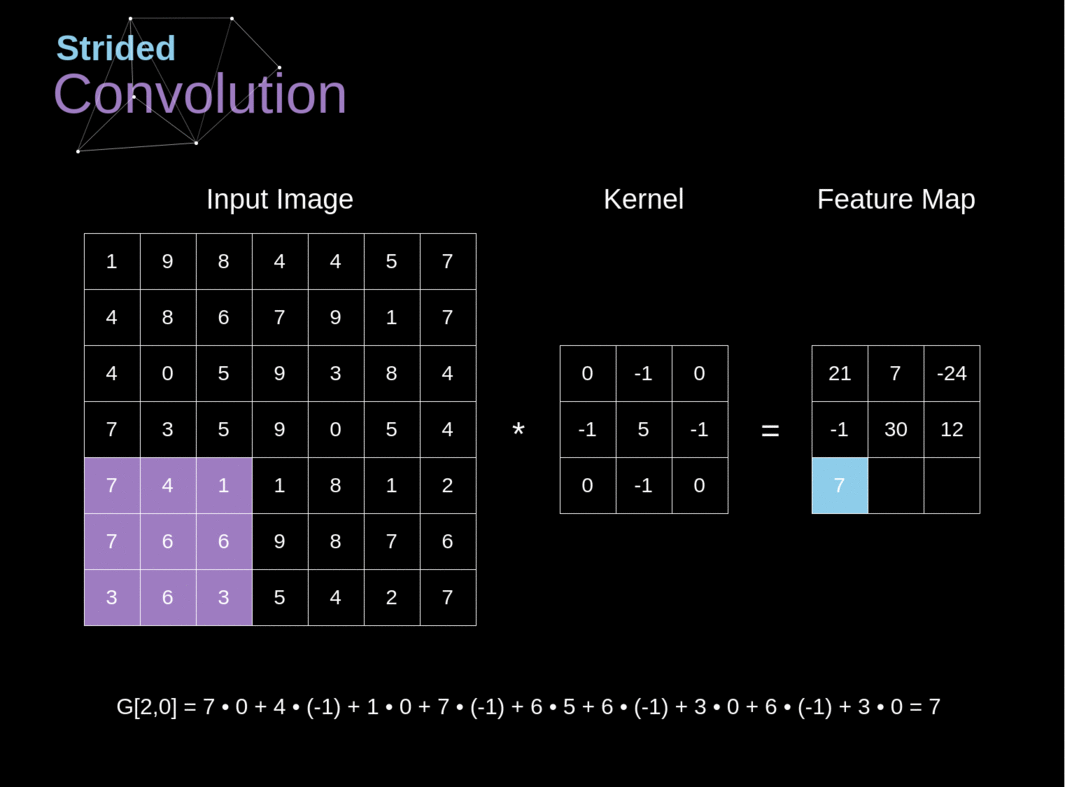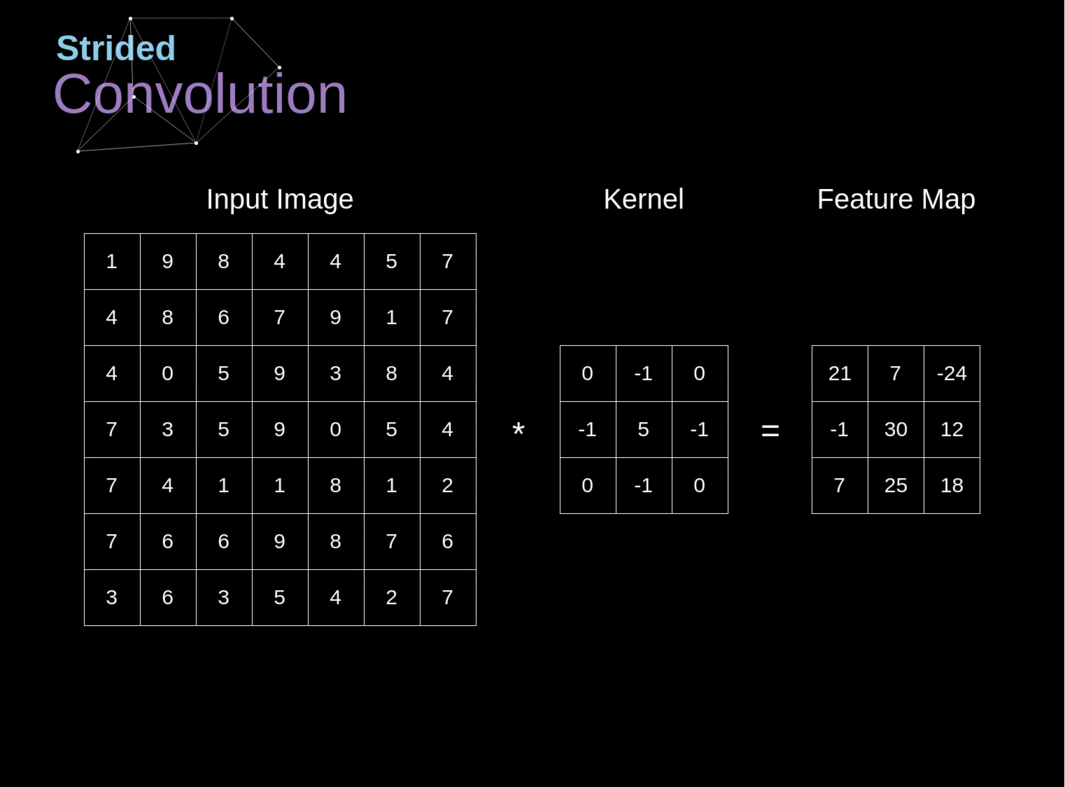 Image credit to https://towardsdatascience.com/gentle-dive-into-math-behind-convolutional-neural-networks-79a07dd44cf9.
Image credit to https://towardsdatascience.com/gentle-dive-into-math-behind-convolutional-neural-networks-79a07dd44cf9.
See also Convolution arithmetic.
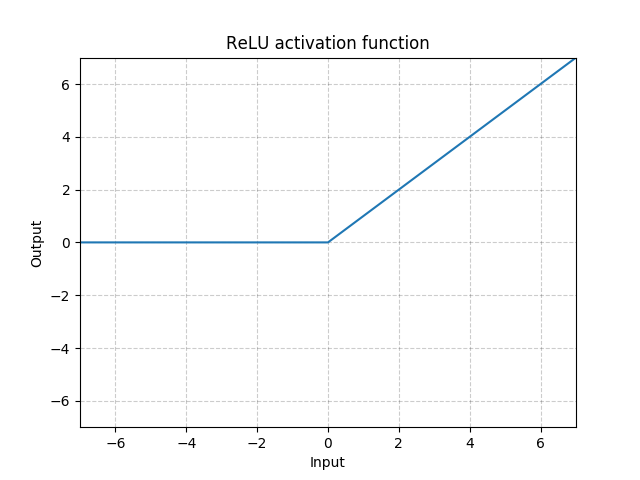 Image credit to https://pytorch.org/docs/stable/nn.html#relu
Image credit to https://pytorch.org/docs/stable/nn.html#relu
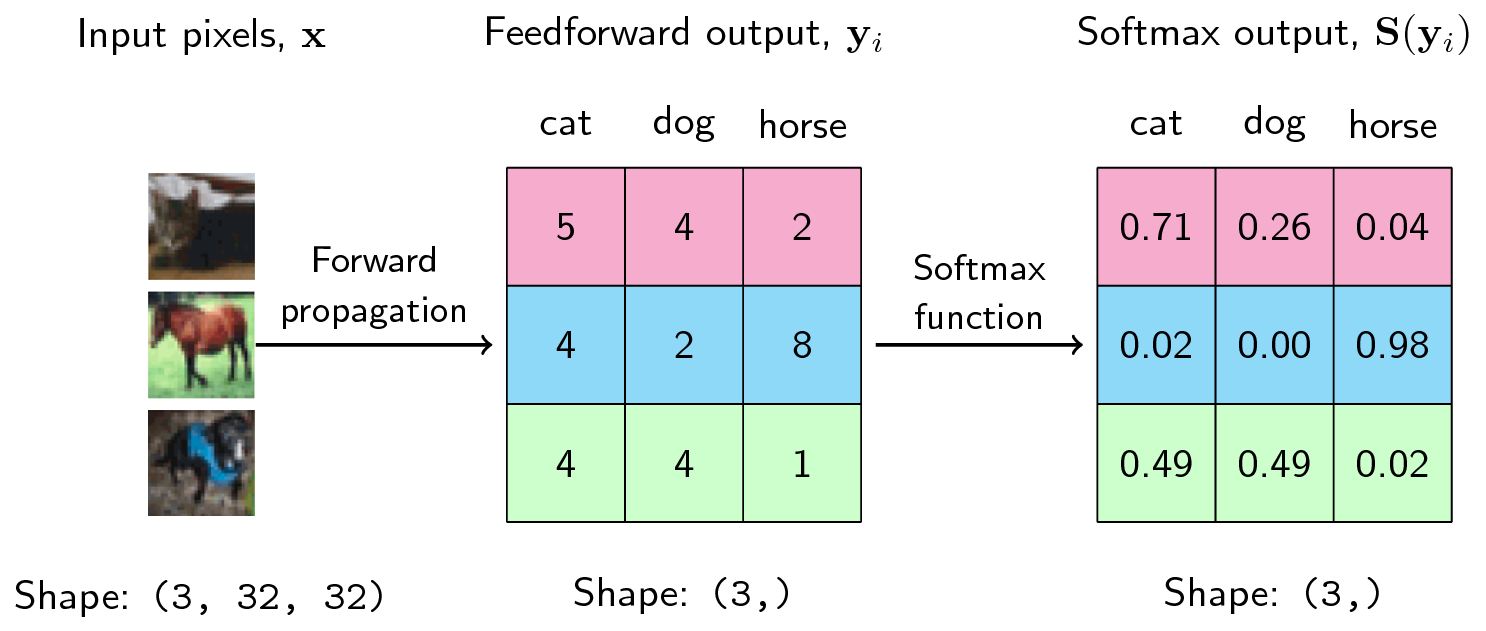 Image credit to https://ljvmiranda921.github.io/notebook/2017/08/13/softmax-and-the-negative-log-likelihood/
Image credit to https://ljvmiranda921.github.io/notebook/2017/08/13/softmax-and-the-negative-log-likelihood/
Even though neural networks are capable of incredible feats of classification, deep down, they really are just pipelines of relatively simple functions. For images, the input is a 2D array of scalar values for gray scale images or RGB triples for colored images. When needed, one can always flatten the 2D array into an equivalent () -dimensional vector. Similarly, the intermediate values after any one of the functions in composition, or activations of neurons after a layer, can also be seen as vectors in , where is the number of neurons in the layer. The softmax, for example, can be seen as a 10-vector whose values are positive real numbers that sum up to 1. This vector view of data in neural network not only allows us represent complex data in a mathematically compact form, but also hints us on how to visualize them in a better way.
Most of the simple functions fall into two categories: they are either linear transformations of their inputs (like fully-connected layers or convolutional layers), or relatively simple non-linear functions that work component-wise (like sigmoid activations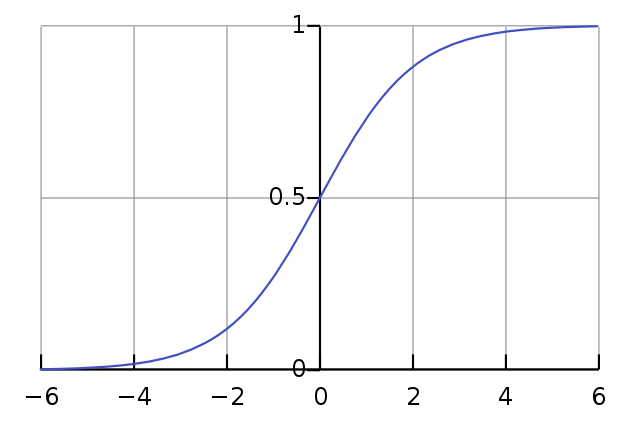 Image credit to https://en.wikipedia.org/wiki/Sigmoid_function
Image credit to https://en.wikipedia.org/wiki/Sigmoid_function
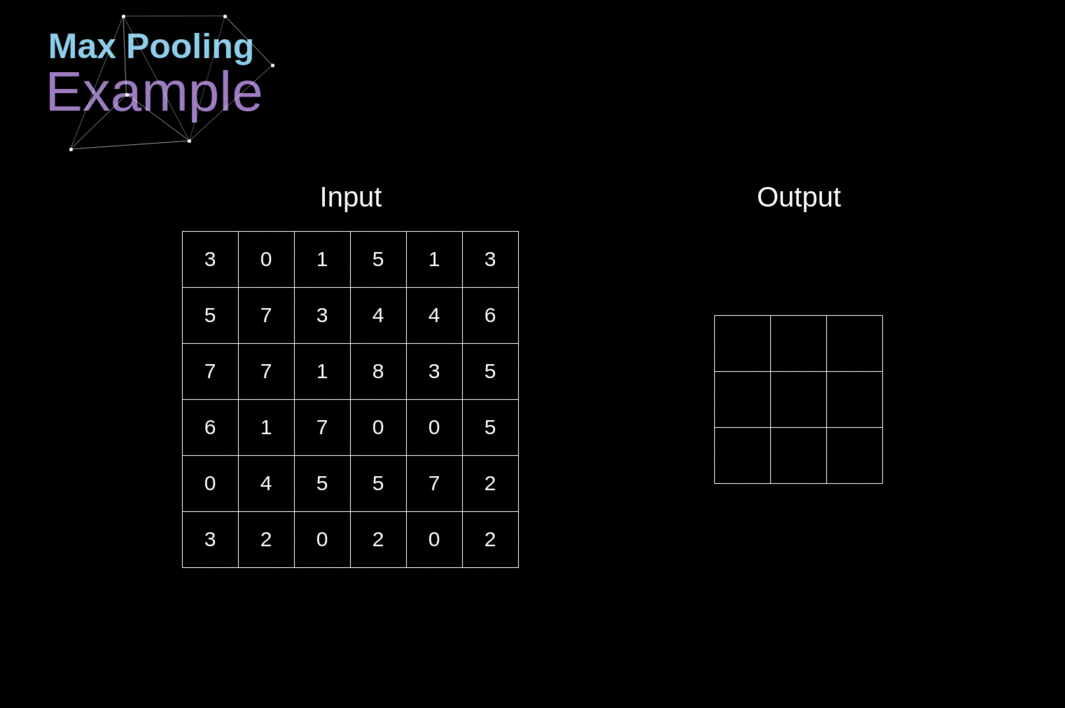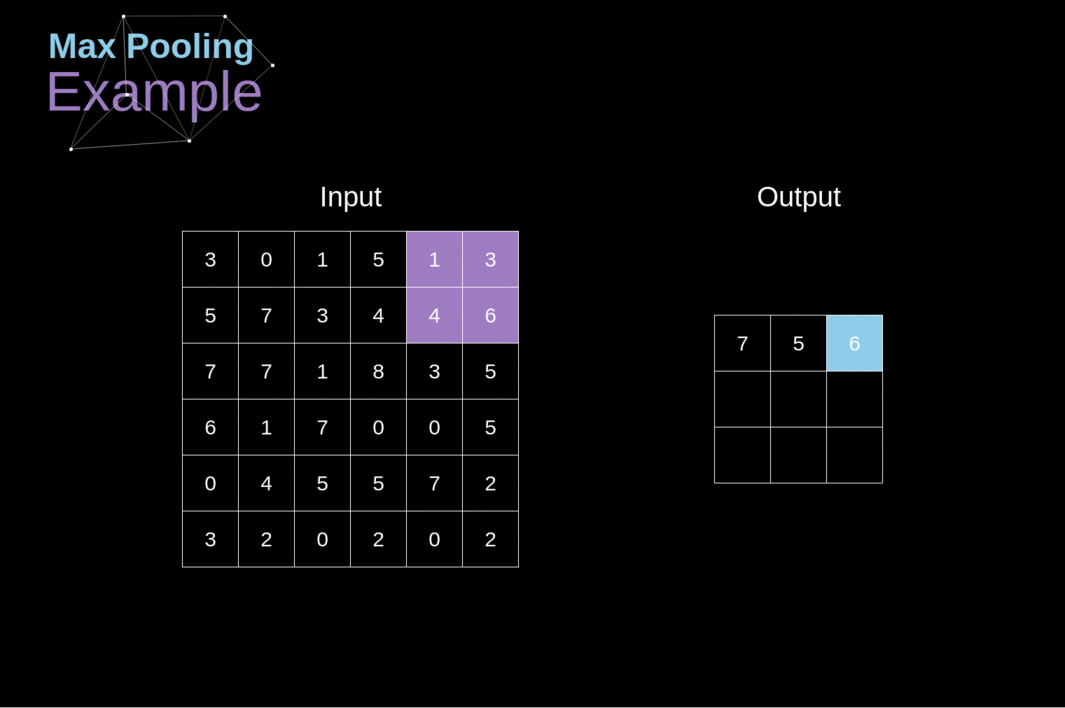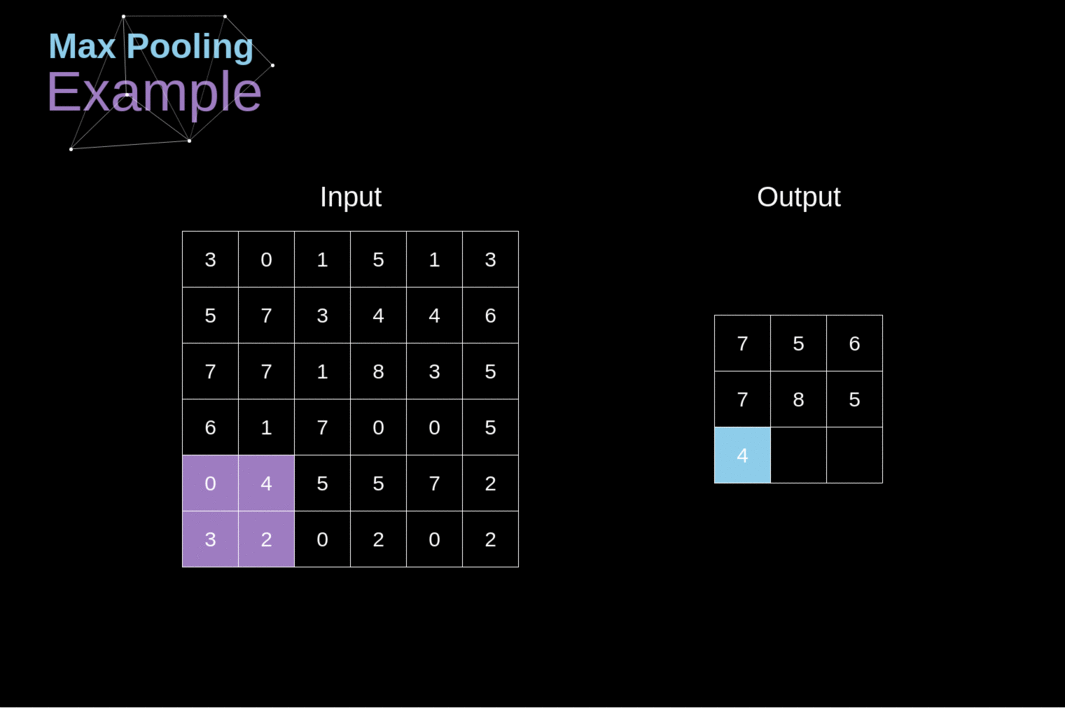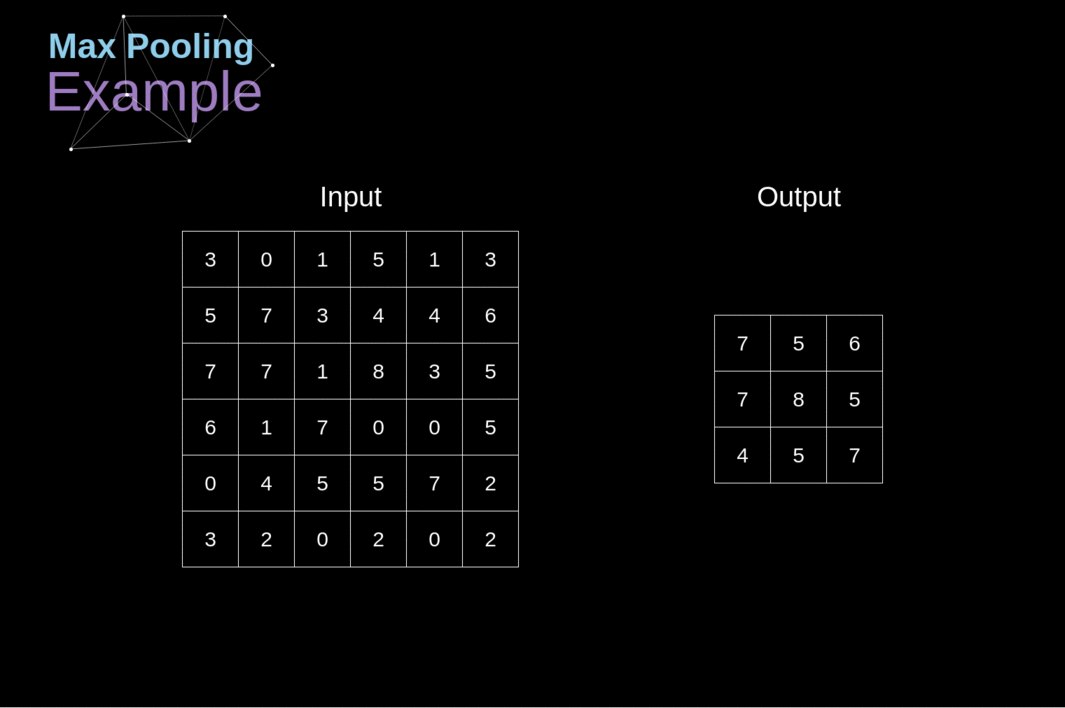 Image credit to https://towardsdatascience.com/gentle-dive-into-math-behind-convolutional-neural-networks-79a07dd44cf9
Image credit to https://towardsdatascience.com/gentle-dive-into-math-behind-convolutional-neural-networks-79a07dd44cf9
The above figure helps us look at a single image at a time; however, it does not provide much context to understand the relationship between layers, between different examples, or between different class labels. For that, researchers often turn to more sophisticated visualizations.
Using Visualization to Understand DNNs
Let’s start by considering the problem of visualizing the training process of a DNN. When training neural networks, we optimize parameters in the function to minimize a scalar-valued loss function, typically through some form of gradient descent. We want the loss to keep decreasing, so we monitor the whole history of training and testing losses over rounds of training (or “epochs”), to make sure that the loss decreases over time. The following figure shows a line plot of the training loss for the MNIST classifier.
Although its general trend meets our expectation as the loss steadily decreases, we see something strange around epochs 14 and 21: the curve goes almost flat before starting to drop again. What happened? What caused that?
If we separate input examples by their true labels/classes and plot the per-class loss like above, we see that the two drops were caused by the classses 1 and 7; the model learns different classes at very different times in the training process. Although the network learns to recognize digits 0, 2, 3, 4, 5, 6, 8 and 9 early on, it is not until epoch 14 that it starts successfully recognizing digit 1, or until epoch 21 that it recognizes digit 7. If we knew ahead of time to be looking for class-specific error rates, then this chart works well. But what if we didn’t really know what to look for?
In that case, we could consider visualizations of neuron activations (e.g. in the last softmax layer) for all examples at once, looking to find patterns like class-specific behavior, and other patterns besides. Should there be only two neurons in that layer, a simple two-dimensional scatter plot would work. However, the points in the softmax layer for our example datasets are 10 dimensional (and in larger-scale classification problems this number can be much larger). We need to either show two dimensions at a time (which does not scale well as the number of possible charts grows quadratically), or we can use dimensionality reduction to map the data into a two dimensional space and show them in a single plot.
The State-of-the-art Dimensionality Reduction is Non-linear
Modern dimensionality reduction techniques such as t-SNE and UMAP are capable of impressive feats of summarization, providing two-dimensional images where similar points tend to be clustered together very effectively.
However, these methods are not particularly good to understand the behavior of neuron activations at a fine scale.
Consider the aforementioned intriguing feature about the different learning rate that the MNIST classifier has on digit 1 and 7: the network did not learn to recognize digit 1 until epoch 14, digit 7 until epoch 21.
We compute t-SNE, Dynamic t-SNE
One reason that non-linear embeddings fail in elucidating this phenomenon is that, for the particular change in the data, the fail the principle of data-visual correspondence
Non-linear embeddings that have non-convex objectives also tend to be sensitive to initial conditions.
For example, in MNIST, although the neural network starts to stabilize on epoch 30, t-SNE and UMAP still generate quite different projections between epochs 30, 31 and 32 (in fact, all the way to 99).
Temporal regularization techniques (such as Dynamic t-SNE) mitigate these consistency issues, but still suffer from other interpretability issues
Now, let’s consider another task, that of identifying classes which the neural network tends to confuse. For this example, we will use the Fashion-MNIST dataset and classifier, and consider the confusion among sandals, sneakers and ankle boots. If we know ahead of time that these three classes are likely to confuse the classifier, then we can directly design an appropriate linear projection, as can be seen in the last row of the following figure (we found this particular projection using both the Grand Tour and the direct manipulation technique we later describe). The pattern in this case is quite salient, forming a triangle. T-SNE, in contrast, incorrectly separates the class clusters (possibly because of an inappropriately-chosen hyperparameter). UMAP successfully isolates the three classes, but even in this case it’s not possible to distinguish between three-way confusion for the classifier in epochs 5 and 10 (portrayed in a linear method by the presence of points near the center of the triangle), and multiple two-way confusions in later epochs (evidences by an “empty” center).
Linear Methods to the Rescue
When given the chance, then, we should prefer methods for which changes in the data produce predictable, visually salient changes in the result, and linear dimensionality reductions often have this property. Here, we revisit the linear projections described above in an interface where the user can easily navigate between different training epochs. In addition, we introduce another useful capability which is only available to linear methods, that of direct manipulation. Each linear projection from dimensions to dimensions can be represented by 2-dimensional vectors which have an intuitive interpretation: they are the vectors that the canonical basis vector in the -dimensional space will be projected to. In the context of projecting the final classification layer, this is especially simple to interpret: they are the destinations of an input that is classified with 100% confidence to any one particular class. If we provide the user with the ability to change these vectors by dragging around user-interface handles, then users can intuitively set up new linear projections.
This setup provides additional nice properties that explain the salient patterns in the previous illustrations. For example, because projections are linear and the coefficients of vectors in the classification layer sum to one, classification outputs that are halfway confident between two classes are projected to vectors that are halfway between the class handles.
This particular property is illustrated clearly in the Fashion-MNIST example below. The model confuses sandals, sneakers and ankle boots, as data points form a triangular shape in the softmax layer.
Examples falling between classes indicate that the model has trouble distinguishing the two, such as sandals vs. sneakers, and sneakers vs. ankle boot classes. Note, however, that this does not happen as much for sandals vs. ankle boots: not many examples fall between these two classes. Moreover, most data points are projected close to the edge of the triangle. This tells us that most confusions happen between two out of the three classes, they are really two-way confusions. Within the same dataset, we can also see pullovers, coats and shirts filling a triangular plane. This is different from the sandal-sneaker-ankle-boot case, as examples not only fall on the boundary of a triangle, but also in its interior: a true three-way confusion. Similarly, in the CIFAR-10 dataset we can see confusion between dogs and cats, airplanes and ships. The mixing pattern in CIFAR-10 is not as clear as in fashion-MNIST, because many more examples are misclassified.
The Grand Tour
In the previous section, we took advantage of the fact that we knew which classes to visualize.
That meant it was easy to design linear projections for the particular tasks at hand.
But what if we don’t know ahead of time which projection to choose from, because we don’t quite know what to look for?
Principal Component Analysis (PCA) is the quintessential linear dimensionality reduction method,
choosing to project the data so as to preserve the most variance possible.
However, the distribution of data in softmax layers often has similar variance along many axis directions, because each axis concentrates a similar number of examples around the class vector.
Starting with a random velocity, it smoothly rotates data points around the origin in high dimensional space, and then projects it down to 2D for display. Here are some examples of how Grand Tour acts on some (low-dimensional) objects:
- On a square, the Grand Tour rotates it with a constant angular velocity.
- On a cube, the Grand Tour rotates it in 3D, and its 2D projection let us see every facet of the cube.
- On a 4D cube (a tesseract), the rotation happens in 4D and the 2D view shows every possible projection.
The Grand Tour of the Softmax Layer
We first look at the Grand Tour of the softmax layer. The softmax layer is relatively easy to understand because its axes have strong semantics. As we described earlier, the -th axis corresponds to network’s confidence about predicting that the given input belongs to the -th class.
The Grand Tour of the softmax layer lets us qualitatively assess the performance of our model. In the particular case of this article, since we used comparable architectures for three datasets, this also allows us to gauge the relative difficulty of classifying each dataset. We can see that data points are most confidently classified for the MNIST dataset, where the digits are close to one of the ten corners of the softmax space. For Fashion-MNIST or CIFAR-10, the separation is not as clean, and more points appear inside the volume.
The Grand Tour of Training Dynamics
Linear projection methods naturally give a formulation that is independent of the input points, allowing us to keep the projection fixed while the data changes. To recap our working example, we trained each of the neural networks for 99 epochs and recorded the entire history of neuron activations on a subset of training and testing examples. We can use the Grand Tour, then, to visualize the actual training process of these networks.
In the beginning when the neural networks are randomly initialized, all examples are placed around the center of the softmax space, with equal weights to each class. Through training, examples move to class vectors in the softmax space. The Grand Tour also lets us compare visualizations of the training and testing data, giving us a qualitative assessment of over-fitting. In the MNIST dataset, the trajectory of testing images through training is consistent with the training set. Data points went directly toward the corner of its true class and all classes are stabilized after about 50 epochs. On the other hand, in CIFAR-10 there is an inconsistency between the training and testing sets. Images from the testing set keep oscillating while most images from training converges to the corresponding class corner. In epoch 99, we can clearly see a difference in distribution between these two sets. This signals that the model overfits the training set and thus does not generalize well to the testing set.
The Grand Tour of Layer Dynamics
Given the presented techniques of the Grand Tour and direct manipulations on the axes, we can in theory visualize and manipulate any intermediate layer of a neural network by itself. Nevertheless, this is not a very satisfying approach, for two reasons:
- In the same way that we’ve kept the projection fixed as the training data changed, we would like to “keep the projection fixed”, as the data moves through the layers in the neural network. However, this is not straightforward. For example, different layers in a neural network have different dimensions. How do we connect rotations of one layer to rotations of the other?
- The class “axis handles” in the softmax layer convenient, but that’s only practical when the dimensionality of the layer is relatively small. With hundreds of dimensions, for example, there would be too many axis handles to naturally interact with. In addition, hidden layers do not have as clear semantics as the softmax layer, so manipulating them would not be as intuitive.
To address the first problem, we will need to pay closer attention to the way in which layers transform the data that they are given. To see how a linear transformation can be visualized in a particularly ineffective way, consider the following (very simple) weights (represented by a matrix ) which take a 2-dimensional hidden layer and produce activations in another 2-dimensional layer . The weights simply negate two activations in 2D: Imagine that we wish to visualize the behavior of network as the data moves from layer to layer. One way to interpolate the source and destination of this action is by a simple linear interpolation for Effectively, this strategy reuses the linear projection coefficients from one layer to the next. This is a natural thought, since they have the same dimension. However, notice the following: the transformation given by A is a simple rotation of the data. Every linear transformation of the layer could be encoded simply as a linear transformation of the layer , if only that transformation operated on the negative values of the entries. In addition, since the Grand Tour has a rotation itself built-in, for every configuration that gives a certain picture of the layer , there exists a different configuration that would yield the same picture for layer , by taking the action of into account. In effect, the naive interpolation fails the principle of data-visual correspondence: a simple change in data (negation in 2D/180 degree rotation) results in a drastic change in visualization (all points cross the origin).
This observation points to a more general strategy: when designing a visualization, we should be as explicit as possible about which parts of the input (or process) we seek to capture in our visualizations. We should seek to explicitly articulate what are purely representational artifacts that we should discard, and what are the real features a visualization we should distill from the representation. Here, we claim that rotational factors in linear transformations of neural networks are significantly less important than other factors such as scalings and nonlinearities. As we will show, the Grand Tour is particularly attractive in this case because it is can be made to be invariant to rotations in data. As a result, the rotational components in the linear transformations of a neural network will be explicitly made invisible.
Concretely, we achieve this by taking advantage of a central theorem of linear algebra.
The Singular Value Decomposition (SVD) theorem shows that any linear transformation can be decomposed into a sequence of very simple operations: a rotation, a scaling, and another rotation
(For the following portion, we reduce the number of data points to 500 and epochs to 50, in order to reduce the amount of data transmitted in a web-based demonstration.) With the linear algebra structure at hand, now we are able to trace behaviors and patterns from the softmax back to previous layers. In fashion-MNIST, for example, we observe a separation of shoes (sandals, sneakers and ankle boots as a group) from all other classes in the softmax layer. Tracing it back to earlier layers, we can see that this separation happened as early as layer 5:
The Grand Tour of Adversarial Dynamics
As a final application scenario, we show how the Grand Tour can also elucidate the behavior of adversarial examples
Through this adversarial training, the network eventually claims, with high confidence, that the inputs given are all 0s. If we stay in the softmax layer and slide though the adversarial training steps in the plot, we can see adversarial examples move from a high score for class 8 to a high score for class 0. Although all adversarial examples are classified as the target class (digit 0s) eventually, some of them detoured somewhere close to the centroid of the space (around the 25th epoch) and then moved towards the target. Comparing the actual images of the two groups, we see those that those “detouring” images tend to be noisier.
More interesting, however, is what happens in the intermediate layers. In pre-softmax, for example, we see that these fake 0s behave differently from the genuine 0s: they live closer to the decision boundary of two classes and form a plane by themselves.
Discussion
Limitations of the Grand Tour
Early on, we compared several state-of-the-art dimensionality reduction techniques with the Grand Tour, showing that non-linear methods do not have as many desirable properties as the Grand Tour for understanding the behavior of neural networks. However, the state-of-the-art non-linear methods come with their own strength. Whenever geometry is concerned, like the case of understanding multi-way confusions in the softmax layer, linear methods are more interpretable because they preserve certain geometrical structures of data in the projection. When topology is the main focus, such as when we want to cluster the data or we need dimensionality reduction for downstream models that are less sensitive to geometry, we might choose non-linear methods such as UMAP or t-SNE for they have more freedom in projecting the data, and will generally make better use of the fewer dimensions available.
The Power of Animation and Direct Manipulation
When comparing linear projections with non-linear dimensionality reductions, we used small multiples to contrast training epochs and dimensionality reduction methods.
The Grand Tour, on the other hand, uses a single animated view.
When comparing small multiples and animations, there is no general consensus on which one is better than the other in the literature, aside.
from specific settings such as dynamic graph drawing
Non-sequential Models
In our work we have used models that are purely “sequential”, in the sense that the layers can be put in numerical ordering, and that the activations for
the -th layer are a function exclusively of the activations at the -th layer.
In recent DNN architectures, however, it is common to have non-sequential parts such as highway
Scaling to Larger Models
Modern architectures are also wide. Especially when convolutional layers are concerned, one could run into issues with scalability if we see such layers as a large sparse matrix acting on flattened multi-channel images.
For the sake of simplicity, in this article we brute-forced the computation of the alignment of such convolutional layers by writing out their explicit matrix representation.
However, the singular value decomposition of multi-channel 2D convolutions can be computed efficiently
Technical Details
Notation
In this section, our notational convention is that data points are represented as row vectors. An entire dataset is laid out as a matrix, where each row is a data point, and each column represents a different feature/dimension. As a result, when a linear transformation is applied to the data, the row vectors (and the data matrix overall) are left-multiplied by the transformation matrix. This has a side benefit that when applying matrix multiplications in a chain, the formula reads from left to right and aligns with a commutative diagram. For example, when a data matrix is multiplied by a matrix to generate , in formula we write , the letters have the same order in diagram:
Furthermore, if the SVD of is , we have , and the diagram nicely aligns with the formula.Direct Manipulation
The direct manipulations we presented earlier provide explicit control over the possible projections for the data points. We provide two modes: directly manipulating class axes (the “axis mode”), or directly manipulating a group of data points through their centroid (the “data point mode”). Based on the dimensionality and axis semantics, as discussed in Layer Dynamics, we may prefer one mode than the other. We will see that the axis mode is a special case of data point mode, because we can view an axis handle as a particular “fictitious” point in the dataset. Because of its simplicity, we will first introduce the axis mode.
The Axis Mode
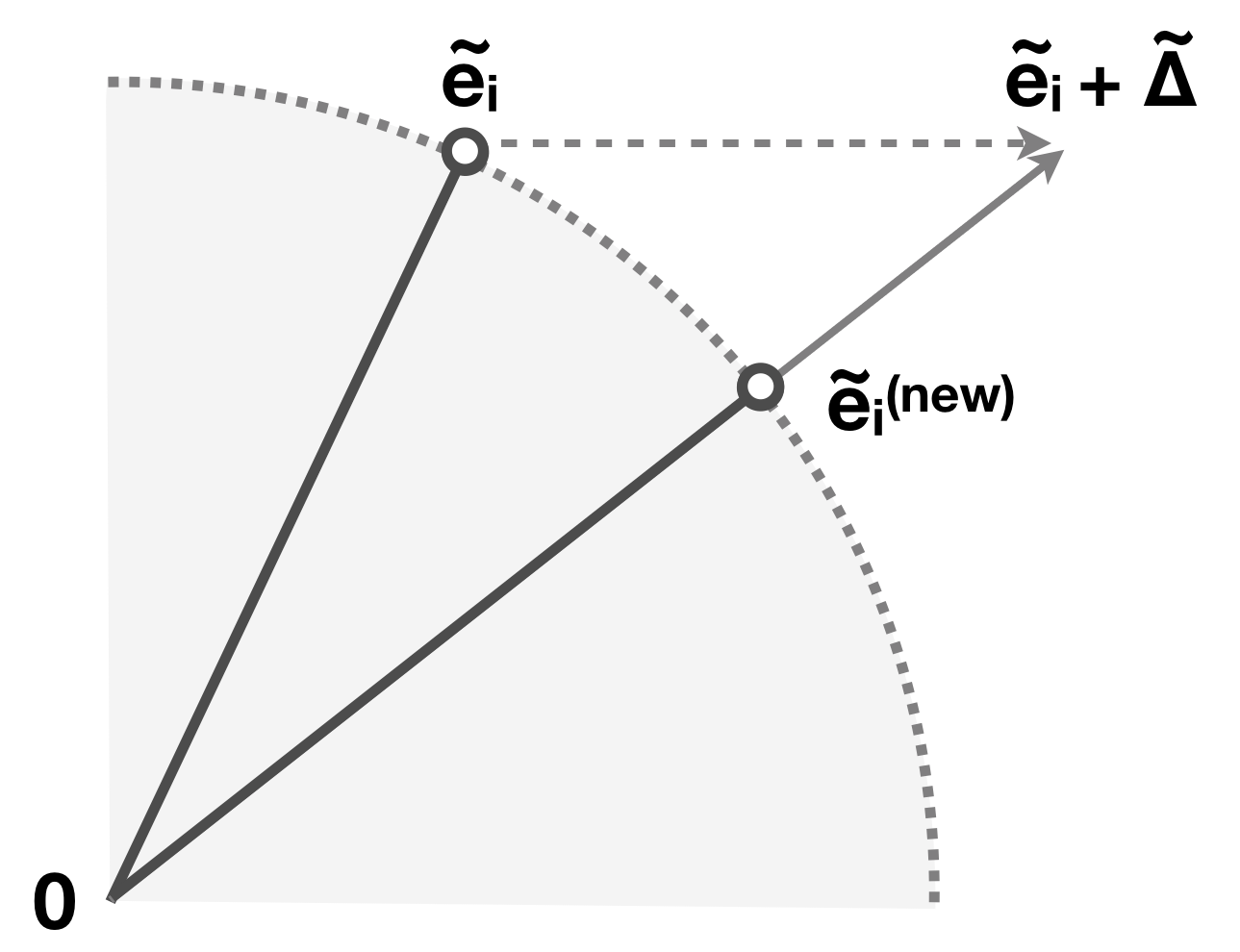
The implied semantics of direct manipulation is that when a user drags an UI element (in this case, an axis handle), they are signaling to the system that they wished that the corresponding
data point had been projected to the location where the UI element was dropped, rather than where it was dragged from.
In our case the overall projection is a rotation (originally determined by the Grand Tour), and an arbitrary user manipulation might not necessarily generate a new projection that is also a rotation. Our goal, then, is to find a new rotation which satisfies the user request and is close to the previous state of the Grand Tour projection, so that the resulting state satisfies the user request.
In a nutshell, when user drags the axis handle by , we add them to the first two entries of the row of the Grand Tour matrix, and then perform Gram-Schmidt orthonormalization on the rows of the new matrix.
Before we see in detail why this works well, let us formalize the process of the Grand Tour on a standard basis vector . As shown in the diagram below, goes through an orthogonal Grand Tour matrix to produce a rotated version of itself, . Then, is a function that keeps only the first two entries of and gives the 2D coordinate of the handle to be shown in the plot, .
When user drags an axis handle on the screen canvas, they induce a delta change on the -plane. The coordinate of the handle becomes: Note that and are the first two coordinates of the axis handle in high dimensions after the Grand Tour rotation, so a delta change on induces a delta change on :
To find a nearby Grand Tour rotation that respects this change, first note that is exactly the row of orthogonal Grand Tour matrix
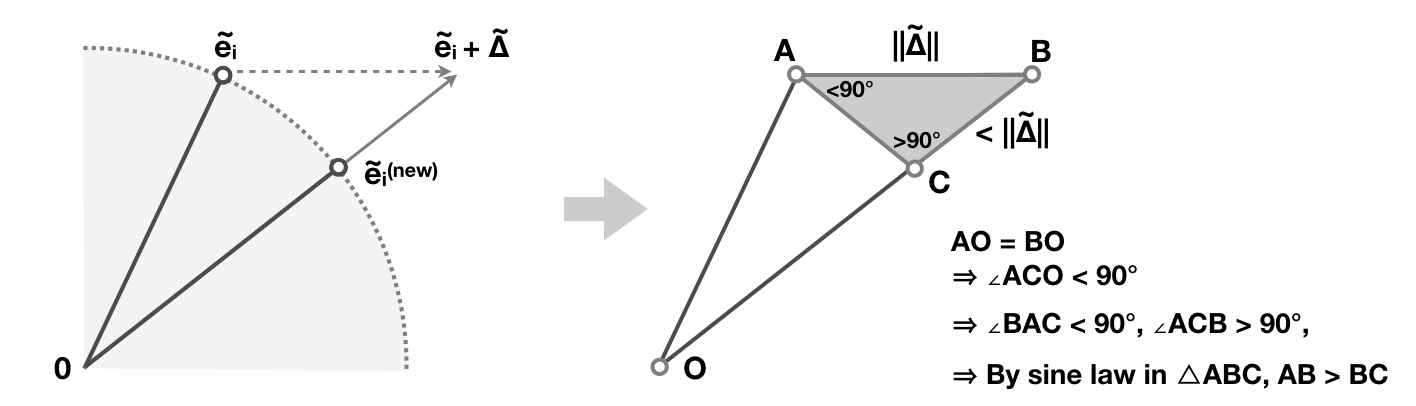
The Data Point Mode
We now explain how we directly manipulate data points. Technically speaking, this method only considers one point at a time. For a group of points, we compute their centroid and directly manipulate this single point with this method. Thinking more carefully about the process in axis mode gives us a way to drag any single point. Recall that in axis mode, we added user’s manipulation to the position of the axis handle . This induces a delta change in the row of the Grand Tour matrix . Next, as the first step in Gram-Schmidt, we normalized this row: These two steps make the axis handle move from to .
Looking at the geometry of this movement, the “add-delta-then-normalize” on is equivalent to a rotation from towards , illustrated in the figure below. This geometric interpretation can be directly generalized to any arbitrary data point.
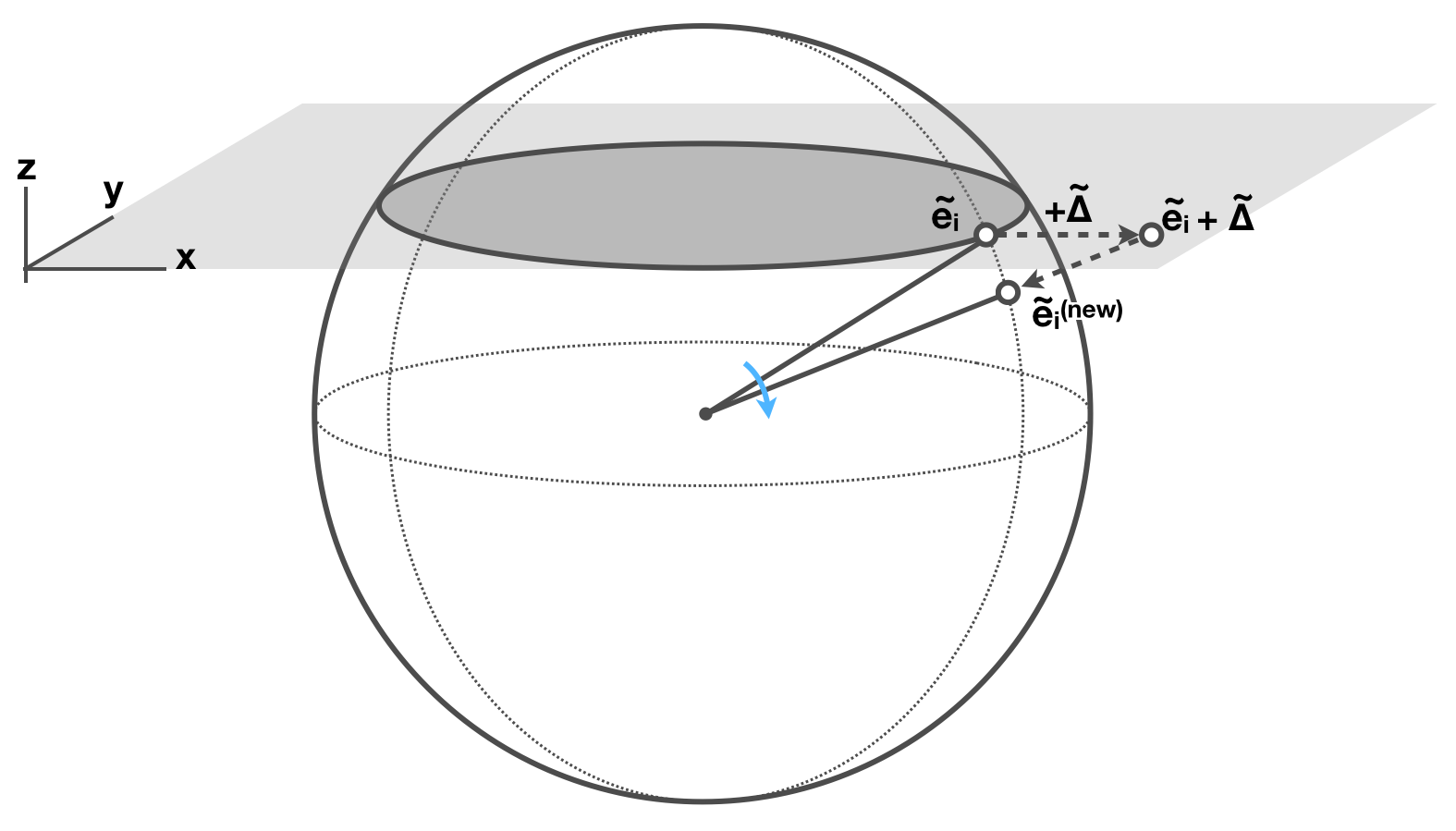
The figure shows the case in 3D, but in higher dimensional space it is essentially the same, since the two vectors and only span a 2-subspace.
Now we have a nice geometric intuition about direct manipulation: dragging a point induces a simple rotation
Generalizing this observation from axis handle to arbitrary data point, we want to find the rotation that moves the centroid of a selected subset of data points to
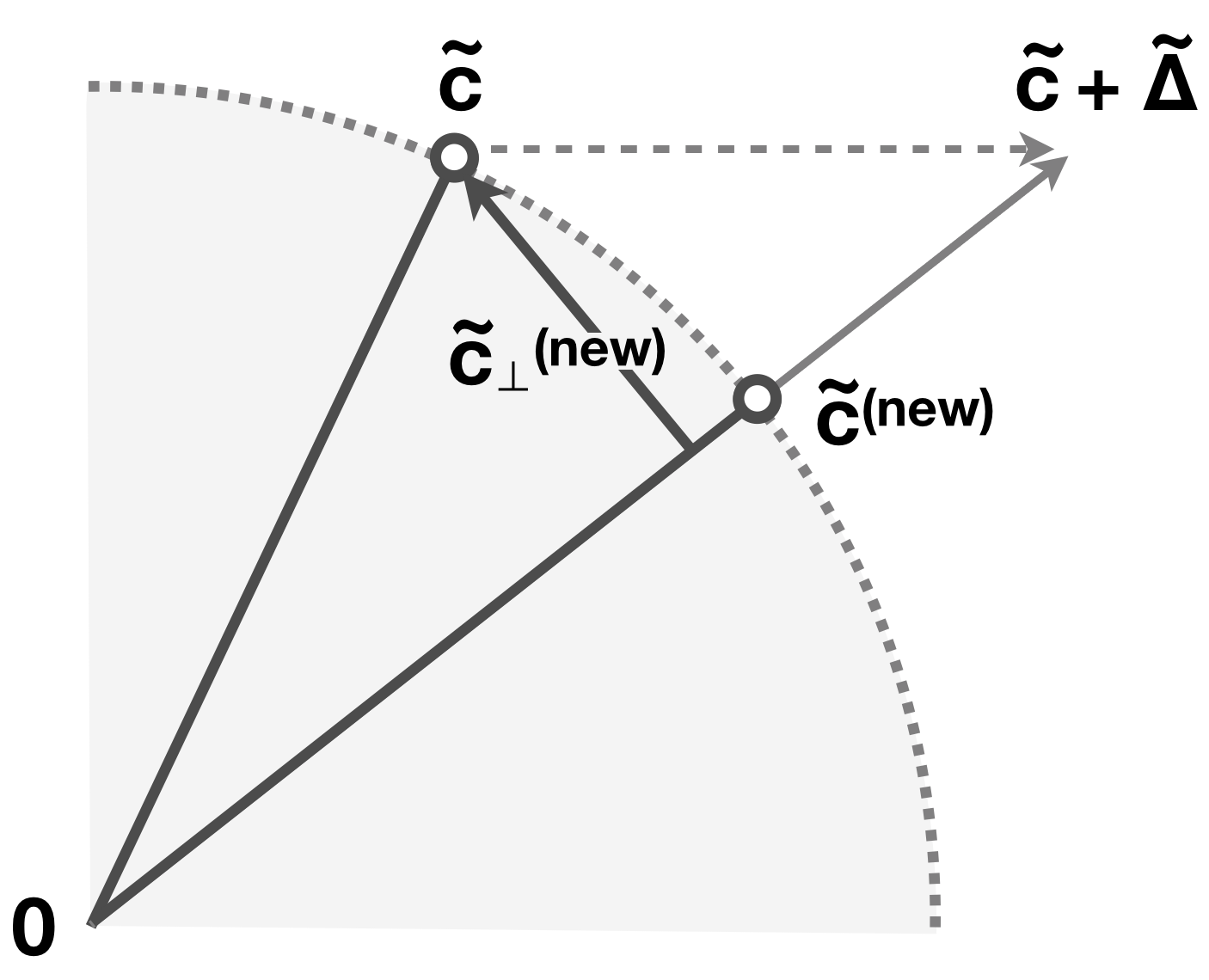
First, the angle of rotation can be found by their cosine similarity: Next, to find the matrix form of the rotation, we need a convenient basis. Let be a change of (orthonormal) basis matrix in which the first two rows form the 2-subspace . For example, we can let its first row to be , second row to be its orthonormal complement in , and the remaining rows complete the whole space: where completes the remaining space. Making use of , we can find the matrix that rotates the plane by the angle : The new Grand Tour matrix is the matrix product of the original and : Now we should be able to see the connection between axis mode and data point mode. In data point mode, finding can be done by Gram-Schmidt: Let the first basis be , find the orthogonal component of in , repeatedly take a random vector, find its orthogonal component to the span of the current basis vectors and add it to the basis set. In axis mode, the -row-first Gram-Schmidt does the rotation and change of basis in one step.
Layer Transitions
ReLU Layers
Linear Layers
Convolutional Layers
Max-pooling Layers
Conclusion
As powerful as t-SNE and UMAP are, they often fail to offer the correspondences we need, and such correspondences can come, surprisingly, from relatively simple methods like the Grand Tour. The Grand Tour method we presented is particularly useful when direct manipulation from the user is available or desirable. We believe that it might be possible to design methods that highlight the best of both worlds, using non-linear dimensionality reduction to create intermediate, relatively low-dimensional representations of the activation layers, and using the Grand Tour and direct manipulation to compute the final projection.